Aula 2 - Exercícios de Sala

1> Durante um espirro, os olhos podem se fechar por até 0,5s. Se você está dirigindo um carro a 90km/h e espirra, de quanto o carro pode se deslocar até você abrir novamente os olhos?

2> Um automóvel viaja em uma estrada reta por 40 km a 30 km/h. Depois, continuando no mesmo sentido, percorre outros 40 km a 60 km/h. Qual é a velocidade média do carro durante essa viagem de 80 km? 

3> Em um certo instante de tempo, uma partícula tinha uma velocidade de 18 m/s no sentido positivo de x, e 2,4 s depois sua velocidade era de 30 m/s no sentido oposto. Qual a aceleração média da partícula durante este intervalo de 2,4 s?

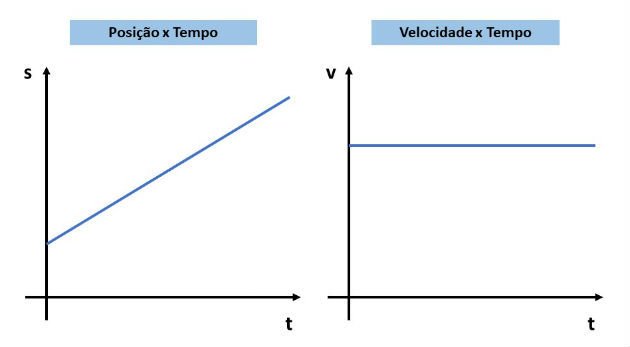
4> Em uma estrada seca, um carro com pneus bons é capaz de frear com uma desaceleração constante de 4,92 m/sˆ2. (a) Quanto tempo um tal carro, inicialmente viajando a 24,6 m/s, leva para parar? (b) Quanto ele se desloca neste tempo? (c) Trace os gráficos s versus t, e v versus t.

Aula 2 - Cinemática - Movimentos

Link para a aula

Em nossa aula 2 estaremos falando de grandezas muito importantes para o movimento. Começaremos definindo espaço e deslocamento e logo após velocidade média e instantânea:

Logo depois passaremos a explicar o conceito de aceleração média e instantânea:

Aplicaremos esses conceitos a vários problemas.

Falaremos sobre a classificação do movimento:

Falaremos do Movimento Uniforme, sua função horária e seus gráficos.

No final mostraremos o Movimento Uniformemente Variado, suas funções e gráficos.

Introdução ao Movimento aula da UNICAMP

Universo Mecânico (Derivadas)

Importante: Teremos exercício valendo pontos durante a aula.

Aula 1 - Exercícios de Sala

1> A componente x do vetor A é -25,0 m e a componente y é +40,0 m. (a) Qual é o módulo de A? (b) Qual é o ângulo entre a orientação de A e o semieixo x positivo?

2> Um carro viaja 50 km para leste, 30 km para o norte e 25 km em uma direção 30º a leste do norte. Desenhe o diagrama vetorial e determine (a) o módulo e (b) o ângulo do deslocamento do carro em relação ao ponto de partida.

3> O módulo do vetor A é de 6,00 unidades, o módulo do vetor B é de 7,00 unidades e A . B = 14,0. Qual é o ângulo entre A e B?

4> Considere dois deslocamentos, um de módulo 3 me outro de módulo 4 m. Mostre que os vetores deslocamento podem ser combinados para produzir um deslocamento de módulo (a) 7 m, (b) 1 m e (c) 5 m.

Aula 1 - Iniciando o Curso

Caros alunos, neste blog vocês encontrarão datas importantes, notas de aula, exercícios, vídeos, dicas para resolução de Trabalhos, revisão para prova, enfim tudo que você precisa para ir bem na disciplina Física Geral e Experimental - Mecânica. Sempre que precisar consulte e no caso de precisar falar comigo envie e-mail.

ruvlemes@anhanguera.com

Neste semestre teremos como atividades avaliatórias:

1º Bimestre

Prova - 1000 Pontos

Atividades de Sala - 700 Pontos

Trabalho - 300 Pontos

2º Bimestre

Prova - 4000 Pontos

Atividades de Sala - 300 Pontos

Trabalho - 1200 Pontos

Medindo Grandezas

Em nossa primeira aula teremos uma discussão sobre o que é uma grandeza, grandezas básicas, como realizar suas medidas e também sobre algarismos significativos e notação científica.

As grandezas básicas: (1) Massa, possui quilograma padrão

(2) Comprimento: Foi utilizado uma barra de platina - irídio:

Hoje:

(3) Segundo: Césio

Falaremos, também de Notação científica e algarismo significativos.

Começaremos o assunto Vetores.

Nessa aula apresentaremos conceitos importantes sobre vetores. Iniciaremos definindo um vetor e aprendendo a escrever em notação de vetor unitário.

Depois discutiremos como determinar o módulo de um vetor.

onde x seria a componente em i e y a componente em j.

Logo depois passaremos a falar sobre o sentido e a direção do vetor e vimos que isso deve ser dado através de um ângulo.

Depois faremos todo o estudo partindo de um vetor que conhecíamos seu módulo e sua direção, com isso determinaremos suas componentes x e y.

Logo depois resolveremos vários exercícios sobre o assunto.

Veja a História de Galileu Galilei:

Universo Mecânico - Introdução: